Chaos Theory: A Deep Dive into Order Within Chaos (pt1)

And how this all relates to the markets.

Chaos theory is a branch of mathematics and science that explores the behavior of dynamic systems highly sensitive to initial conditions – a concept famously referred to as the "butterfly effect." – you might’ve heard of “a butterfly that flaps its wings in Brazil, which causes a hurricane in Japan”, or something along those lines.

The term "chaos" might suggest randomness or disorder, but chaos theory reveals that there is an underlying order in seemingly unpredictable systems. From weather patterns to financial markets, chaotic systems exhibit patterns and structures that, while difficult to predict precisely, follow deterministic rules.

This section explores the origins, principles, and applications of chaos theory, emphasizing its relevance to the financial markets and trading strategies.

Origins and Foundations of Chaos Theory

Chaos theory emerged in the mid-20th century as scientists sought to understand systems that seemed inherently unpredictable. The pivotal moment occurred in 1961 when meteorologist Edward Lorenz discovered what would later be called the "butterfly effect." Using a simple computer model to simulate weather patterns, Lorenz found that even minute changes in initial conditions could lead to vastly different outcomes.

This discovery challenged the classical deterministic view of physics, which held that the future behavior of a system could be predicted with absolute certainty if its initial conditions were known. Instead, Lorenz's work suggested that some systems, though deterministic, are incredibly sensitive to small changes – making long-term prediction virtually impossible.

Key Concepts in Chaos Theory

Sensitivity to Initial Conditions (The Butterfly Effect)

• Small differences in the starting point of a system can lead to exponentially different outcomes over time.
  Example: A butterfly flapping its wings in Brazil could set off a chain reaction culminating in a tornado in Texas.

• In markets: A minor news event or a single trader’s action can ripple through the market, leading to significant price movements.

Deterministic Chaos

• Chaotic systems follow deterministic laws, meaning their behavior is governed by specific rules or equations. However, their complexity makes their long-term behavior appear random.
  Example: The double pendulum, which moves in an unpredictable yet rule-bound manner.

• In markets: Price movements are influenced by supply, demand, and external factors, creating patterns that appear random but are driven by underlying economic principles.

Strange Attractors

• A strange attractor is a set of values toward which a system tends to evolve over time, despite its chaotic behavior. These attractors help define the system's structure and limit its randomness.
  Example: The Lorenz attractor, a three-dimensional structure representing weather patterns.

• In markets: Prices often revolve around specific support and resistance levels, behaving chaotically within these bounds.

Self-Similarity and Fractals

• Chaotic systems often exhibit fractal structures, where patterns repeat at different scales.
  Example: The Mandelbrot set, a famous fractal, demonstrates infinite complexity within a finite space.

• In markets: Price charts show self-similarity across timeframes; patterns observed on a daily chart can also appear on hourly or minute charts.

Nonlinearity

• Chaotic systems are nonlinear, meaning their output is not proportional to their input. Small changes can have outsized effects, and interactions between components create complexity.

• In markets: Nonlinearity explains phenomena like bubbles and crashes, where small triggers lead to dramatic price shifts.

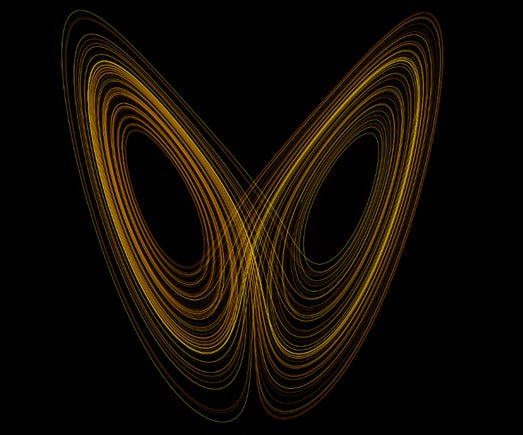
Visualizing Chaos: Lorenz Attractor

Figure 1- Lorenz Attractor

The Lorenz attractor is one of the most iconic images of chaos theory. It consists of two swirling loops that never intersect, representing the trajectory of a system over time. Despite the seemingly erratic movement, the system remains bounded within the attractor.

This visualization is particularly relevant to markets, as it mirrors how price movements can appear erratic yet stay within certain bounds (e.g., support and resistance zones).

Chaos Theory & The Financial Markets

You might be scratching your head by now wondering how this all correlates to the market. The truth is, it’s more important to know than you think.

Financial markets are